¿Qué tiene de visual el razonamiento diagramático en Geometría Euclideana?
Según Kant, nuestro conocimiento geométrico, a diferencia del conocimiento aritmético y analítico, está basado en nuestra intuición espacial. Esta hipótesis puede ponerse a prueba desde diferentes perspectivas, como la histórico-filosófica. Desde esta perspectiva, la idea es que si nuestro conocimiento matemático efectivamente está basado en intuiciones espaciales debe haber algo en la manera como de hecho hacemos geometría en la que debe manifestarse cómo, de hecho, apelamos a dicha intuición espacial. Tradicionalmente se ha pensado que el lugar donde más claramente puede verse esto es en los diagramas de la geometría Euclideana. Si, de hecho, la manera en que apelamos a los diagramas en pruebas geométricas Euclideanas involucra intuición espacial, entonces es cierto que nuestro conocimiento geométrico está basado en ella.
En años recientes, han aparecido muchas trabajos recientes en esta dirección (principalmente por parte de Kenneth Manders, Marco Panza y Danielle Macbeth) y el consenso es que sí: de hecho, la intuición espacial sí figura prominentemente en nuestro uso de diagramas en pruebas de Geometria Euclideana. Sin embargo, esto solo demuestra la verdad de la mitad de la hipótesis, también es necesario determinar si esto es algo peculiar de la geometría Euclidiana o no, es decir, es necesario investigar si lo que se ha dicho sobre diagramas no puede decirse también de formulas y otro tipo de representaciones que también se usan en matemáticas, como los numerales. Tradicionalmente se piensa que formulas y diagramas son radicalmente distintos y que solo los segundos son visuales y por lo tanto, requieren de cierta intuición espacial. Sin embargo, al analizar más de cerca nuestro uso de formulas es claro que las cosas no son tan simples.
Nuestra percepción visual juega dos papeles importantes en este tipo de razonamientos:
- Un papel ergonómico: Usamos círculos – o, mas bien, curvas cerradas muy cercanas a un círculo – para representar círculos, por ejemplo, porque esto nos ayuda a recordar que representan círculos. En general, cuando es posible, en los diagramas Euclideanos se usan figuras que se asemejan visualmente a lo que representan con el propósito de permitirnos usar la percepción visual como mecanismo mnemotécnico para recordar qué representa qué.
- Un papel lógico: Usamos nuestra intuición espacial para identificar y manipular los componentes significativos de los diagramas Euclideanos. Los diagramas forman parte de un sistema de resolución de problemas analítico-sintético, donde se razona no acerca de los diagramas, sino en los diagramas, y para lograr esto, es necesario que podamos percibir la identidad y otras propiedades topológicas (pero no métricas) de los diagramas.
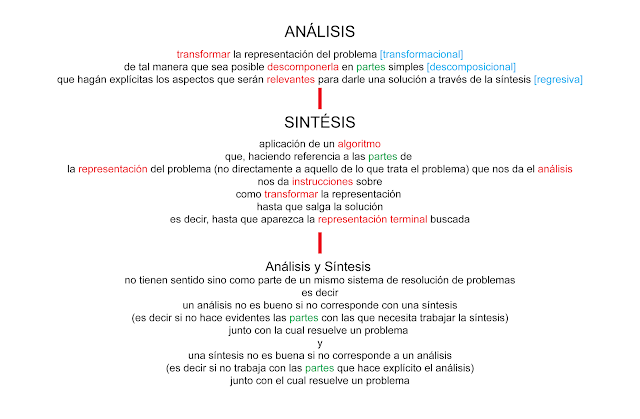
El método analítico-sintético consta de dos partes complementarias, ambas esenciales: el análisis y la síntesis. En el análisis, se busca representar el problema [a esto se le conoce como su dimensión transformacional] de tal manera que sea fácil identificar visualmente sus partes [a esto se le conoce como su dimensión descomposicional] que hagan explícitas los aspectos que serán relevantes para darle una solución a través de la síntesis [a esto se le conoce como su dimensión regresiva]. La síntesis, a su vez, consiste en la aplicación de un algoritmo que nos da instrucciones sobre como transformar la representación que nos da el análisis, a partir de reglas básicas de transformación que hagan referencia sólo a las partes de la representación que obtuvimos a través del análisis (y que, por lo tanto, son fáciles de identificar visualmente), no directamente a aquello de lo que trata el problema, hasta que salga, es decir, hasta que sea fácil identificar visualmente la solución al problema, es decir, hasta que aparezca [lo que Danielle Macbeth ha llamado el “pop up”] lo que Kripke llamó la representación terminal que buscábamos. Análisis y Síntesis no tienen sentido sino como parte de un mismo sistema de resolución de problemas: un análisis no es bueno si no corresponde con una síntesis (es decir si no hace evidentes las partes con las que necesita trabajar la síntesis) junto con la cual resuelve un problema y una síntesis no es buena si no corresponde a un análisis (es decir si no trabaja con las partes que hace explícito el análisis) junto con el cual resuelve un problema. Además, como he acentuado en mi presentación, tanto el análisis como la síntesis tienen un elemento visual central.
Desafortunadamente, la propiedad (2) no es exclusiva de los diagramas de la Geometría Euclideana. Aun más, (2) tampoco captura lo que es distintivamente visual de los diagramas, ya que no se da en todo tipo de diagramas ni sólo en los diagramas. Danielle Macbeth reconoce ya que algunos diagramas, por ejemplo, los aritméticos, no pertenecen a un sistema analítico-sintético como el de los diagrams Euclideanos, pero también señala que hay otros ejemplos que sí funcionan de manera análoga, como el sistema que Frege desarrolla para la lógica en la Conceptografía. Sin embargo, en clase vimos que los numerales y las formulas – ejemplos paradigmáticos de representaciones no-diagramáticas – también se usan para resolver problemas de manera analítico-sintética. Por ejemplo, la manera en que comúnmente calculamos multiplicaciones de enteros positivos de mas de un dígito es del tipo análisis-síntesis: en el análisis se representa la multiplicación usando la numeración arábica (en la cual es fácil de identificar visualmente sus componentes, es decir, los dígitos) poniendo los numerales que corresponden a los multiplicandos uno sobre el otro de tal manera que sus dígitos correspondientes a las unidades se encuentren uno sobre el otro (y, por lo tanto, lo mismo suceda con los dígitos que corresponden a las decenas, centenas, etc.). Esta manera de representar el problema sólo tiene sentido porque nos permite aplicar el algoritmo usual en el que vamos añadiendo numerales, aplicándoles operaciones básicas de suma y multiplicación hasta que aparece (es decir, hasta que se vuelve fácil de identificar visualmente), poco a poco, el numeral que corresponde al producto que buscábamos.
Este proceso es tan visual y exactamente en el mismo sentido que una prueba geométrica Euclideana. Por lo tanto, no podemos decir que (2) sea característico de los diagramas. (1), sin embargo, parece un mejor candidato de lo qué es específicamente visual de los diagramas, ya que ni los numerales ni las formulas explotan la semejanza visual para ayudarnos a recordar qué significa cada símbolo. En otras palabras, ni los numerales ni las formulas se asemejan visualmente a aquello que representan.
Este proceso es tan visual y exactamente en el mismo sentido que una prueba geométrica Euclideana. Por lo tanto, no podemos decir que (2) sea característico de los diagramas. (1), sin embargo, parece un mejor candidato de lo qué es específicamente visual de los diagramas, ya que ni los numerales ni las formulas explotan la semejanza visual para ayudarnos a recordar qué significa cada símbolo. En otras palabras, ni los numerales ni las formulas se asemejan visualmente a aquello que representan.



Comentarios
Publicar un comentario